In this package, synthetic sequencing data are generated using a statistical model for an individual in a given population. Each individual is assigned a COI value, which is used to simulate the number of sequence reads mapped to the reference and alternative allele for the biallelic SNPs considered. These are then used to derive the within-sample frequency of the population-level minor allele at each locus \(i\), denoted as \(w_i\).
We first define the number of loci being simulated, \(l\). We assume that the distribution of reference allele frequencies for locus \(i\), \(R_i\), is described by a Beta distribution with shape parameters \(\alpha\) and \(\beta\): \[ \mathbb{P}(R_i = r_i) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}r_i^{(\alpha-1)}(1-r_i)^{(\beta-1)}, \]
where \(\Gamma\) is the Gamma function. In our simulations, we assume \(\alpha = 1\) and \(\beta = 5\) and draw \(l\) values of \(R_i\). In our methods, we have defined relationships with respect to the frequency of the minor allele, \(p_i\). Recall that \(p_i \in [0, 0.5]\). Thus, we define \[ p_i = \begin{cases} r_i & r_i \leq 0.5 \\ 1 - r_i & r_i > 0.5. \end{cases} \]
To simulate \(w_i\) for each individual, we first assign the COI, \(k\). Next, we simulate the genotype at locus \(i\), drawing \(k\) values from a Binomial distribution with probability \(p_i\), i.e., the probability of having the minor allele at locus \(i\) is equal to the population-level frequency of the minor allele. This yields the matrix, \(\mathbb{G} \in \mathbb{R}^{k \times l}\), with \(k\) rows and \(l\) columns defining the phased haplotype of each strain, where \(\mathbb{G}_{i,j} = 1\) indicates that strain \(j\) at locus \(i\) has the minor allele.
To determine the number of sequence reads related to each strain, we first draw the proportion of each strain, \(\mathbf{S} = (S_1, \ldots, S_k)\), in an individual with \(k\) strains, which we assume is described by a Dirichlet distribution with concentration parameters \(\alpha_1, \ldots, \alpha_k\). The “true” WSMAF of the minor allele at locus \(i\), denoted \(\tau_i\), is thus given by the sum of the strain proportions for strains with the minor allele. We can express this using matrix multiplication: \[ \boldsymbol \tau = \mathbf{S} \times \mathbb{G}_i, \] where \(\boldsymbol \tau \in \mathbb{R}^{1 \times l}\), \(\mathbf{S} \in \mathbb{R}^{1 \times k}\), and \(\mathbb{G} \in \mathbb{R}^{k \times l}\).
In simulations with no assumed sequence error, the number of sequence reads with the minor allele at each locus is given by sampling from a Binomial distribution \(c\) times with probability \(\boldsymbol \tau\), where \(c\) is the assumed number of sequence reads, i.e., the read depth or coverage. However, in simulations with sequence error, we perturb the “true” WSMAF by assuming that a number of sequence reads are incorrectly sampled. An incorrectly sampled locus with the major allele will yield the minor allele and vice versa. In our simulations, we assume a fixed sequence error, \(\epsilon\), such that the probability of correctly sampling the minor allele is \(1 - \epsilon\), and the probability of incorrectly sampling the minor allele is \(\epsilon\). Therefore, we can represent the probability of sampling the minor allele, now denoted as \(\boldsymbol{\tau}_\epsilon\) to indicate the added error, as \[ \boldsymbol{\tau}_\epsilon = \boldsymbol \tau(1 - \epsilon) + (1 - \boldsymbol \tau)\epsilon. \]
Lastly, we may account for overdispersion—additional unexpected variability in our data—and sample the number of sequence reads with the minor allele at each locus from a Beta-binomial distribution rather than a Binomial distribution. Dividing the number of instances of the minor allele by the coverage at each locus results in the simulated WSMAF.
Example simulation
Our package defines a function sim_biallelic() which can
easily be used to simulate data for a given sample. To use it, the user
may simply specify the COI of the simulated sample and the population
level minor allele frequency (PLMAF). The outputs of this function
include the phased haplotypes and the within sample minor allele
frequencies (WSMAF) at each locus.
simulation <- sim_biallelic(2, plmaf = runif(1000, 0, 0.5))
plot(simulation)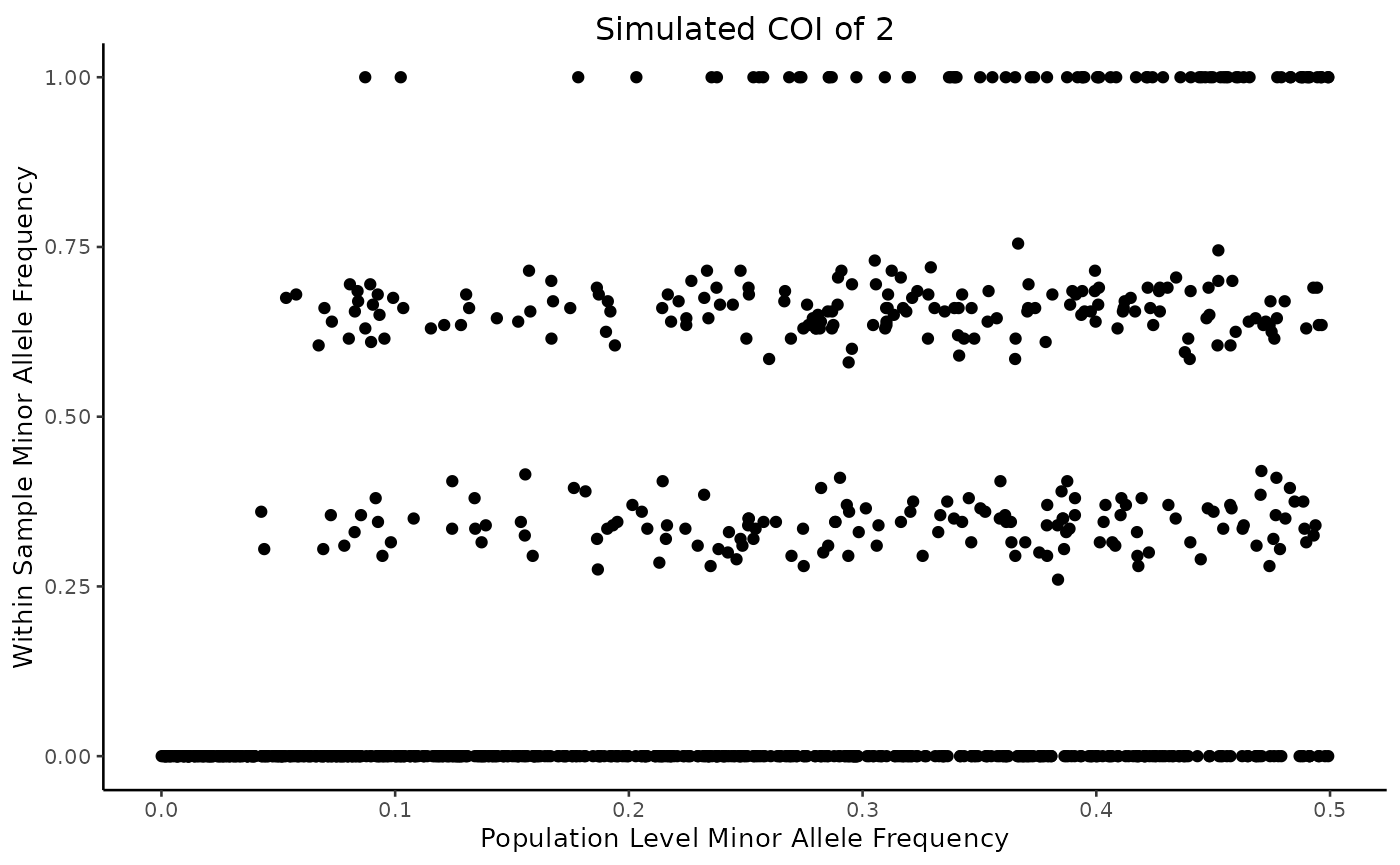
Internally, the function goes through several steps to generate the final output. The first step in generating simulated data is to generate the population level minor allele frequency (PLMAF). To do so, we sample from a Beta distribution.
# Set the seed
set.seed(1)
# Define number of loci and the PLMAF
n_loci <- 5
plmaf <- rbeta(n_loci, 1, 5)
plmaf[plmaf > 0.5] <- 1 - plmaf[plmaf > 0.5]| Locus 1 | Locus 2 | Locus 3 | Locus 4 | Locus 5 |
|---|---|---|---|---|
| 0.356 | 0.13 | 0.012 | 0.105 | 0.435 |
In cases in which the COI is greater than 1, we will have multiple strains of differing proportions in our sample. In order to determine the proportion of each strain present in our sample, we sample from a Dirichlet distribution.
strain_p <- coiaf:::rdirichlet(rep(alpha, COI))| Proportion | |
|---|---|
| Strain 1 | 0.296 |
| Strain 2 | 0.379 |
| Strain 3 | 0.324 |
In order to determine the within sample minor allele frequency (WSMAF) at each locus, we must determine the phased haplotype of each strain. To do so, we draw from a Binomial distribution with probabilities given by the PLMAF.
| Locus 1 | Locus 2 | Locus 3 | Locus 4 | Locus 5 | |
|---|---|---|---|---|---|
| Strain 1 | 0 | 0 | 0 | 0 | 0 |
| Strain 2 | 1 | 0 | 0 | 0 | 1 |
| Strain 3 | 1 | 0 | 0 | 0 | 0 |
To determine the true WSMAF, we can simply combine our haplotype information with our strain proportions—finding the sum of the strain proportions for strains with the minor allele at a particular locus.
true_wsmaf <- colSums(sweep(haplotype, 1, strain_p, "*"))
# Rounding errors can cause numbers greater than 1
true_wsmaf[true_wsmaf > 1] <- 1L| Locus 1 | Locus 2 | Locus 3 | Locus 4 | Locus 5 | |
|---|---|---|---|---|---|
| WSMAF | 0.704 | 0 | 0 | 0 | 0.379 |
Lastly, to generate our final simulated WSMAF we account for sequencing error, sample the number of sequence reads with the minor allele at each locus, and determine the WSMAF by dividing the number of reads with the minor allele by the coverage at each locus.
# Account for sequencing error
true_wsmaf <- true_wsmaf * (1 - epsilon) + (1 - true_wsmaf) * epsilon
# Sample sequence reads
counts <- rbinom(n_loci, size = rep(coverage, n_loci), prob = true_wsmaf)
# Determine simulated WSMAF
sim_wsmaf <- counts / coverage| Locus 1 | Locus 2 | Locus 3 | Locus 4 | Locus 5 | |
|---|---|---|---|---|---|
| WSMAF | 0.73 | 0 | 0 | 0 | 0.35 |
